As Price Reaches Record Highs, is Bitcoin in a Capacity Crisis? — CryptoCoinsNews
Imagine you are slightly late for work, quickly getting a shower, brushing your teeth and all the rest, walking — in an almost running manner — to the tube station, to then find out there are 200,000 people waiting outside to get the train.
What’s more, the train only handles 4,000 individuals and arrives every ten minutes, during which period new individuals arrive at a rate of 4 per second. Now, it’s ok, you’re busy, you can still be one of those 4,000 individuals and get to work if you pay a high enough fee.
So you check out the notice which says the current estimated fee is $1, but since others are seeing the same notice too and paying $1 too, the fee keeps going up every second, with these higher fees paid by the new individuals that come every second, pushing you down the queue.
Tough luck, you can’t make it to work today because your $1 bid is now as good as worthless to the super congested network. The next day you learn the lesson, so instead of bidding what the notice says, you bid 10% or 20% more, but you weren’t the only one who missed work yesterday, almost everyone else did too and they have this genius but obvious idea too, making you miss work again.
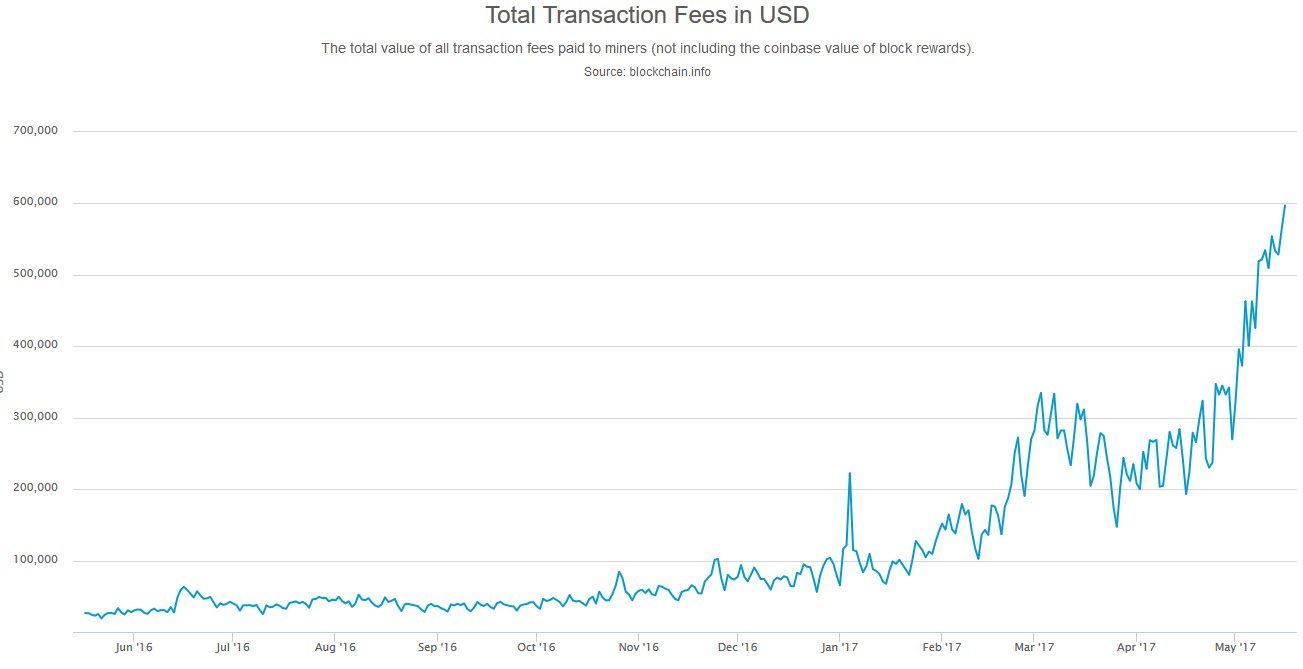
The next day you get angry and pay double the fee, but you’re not the only angry one. Now, sure, some in this lottery do get to make it to work, 4,000 every 10 minutes with 200,000 waiting, but a lot don’t, resulting in a bidding war which looks like below:
As can be seen, bitcoin’s fees have gone vertical, which is bad, but if you know you’d get through for x dollars then at least you can evaluate the proposition. Instead, you’re not only paying high fees, but you don’t even know whether you will get the service you paid for because of simple logics.
Let’s take, for example, a statement by Luke Dashjr, a Blockstream “open hash contractor,” who suggested everyone pay a $5 fee and you’ll get through. If we analyze this a bit further, we can start by asking why people are not paying $5 and one good reason is because then everyone would start paying $5 meaning newcomers would outbid them by paying $5.01.
Sure, one or two guys might currently “cheat” and jump the queue by paying $5, but as long as it’s a very tiny minority the rest let it go. If instead, it went to a point where say 1,000 of the 4,000 are paying $5, the other 3,000 will probably quickly start paying $5.01.
This clearly shows ordering transactions by fee is an unworkable idea which is why Satoshi Nakamoto ordered transactions by first seen in the bitcoin clients he/she released, a rule largely enforced by the bitcoin network until full capacity was reached.
The Easy Attack
Still, even the above problems, as bad as they are, might be bearable for desperate bitcoiners, but let’s imagine I’m a wealthy company, say Vusa, or Rapp Labs, or a wealthy guy who just doesn’t like bitcoin.
Just to be very clear, no one is suggesting either of them has behaved in any nefarious way, but say I’m a competitor to bitcoin or recently attracting much hype and attention due to gaining crazy high market cap in just days. You know what I could do with just $2 million?
I could send bitcoin down crashing as far as its sole purpose of moving bitcoins is concerned. That’s because bitcoin’s capacity is limited to around 250,000 transactions, but just to make it simple let’s say it can handle only 200,000 transactions a day.
At $1, it would cost me just $200,000 to take up that space, which is fine, everyone else could pay $1.50. But, at $10 per transaction it would cost me only $2 million to send everyone else at the back of the queue.
Now sure, you can pay $11 or $12, but even at a fee of $20 it would cost just $4 million, as good as nothing considering how much value may flood to the competitors and considering the shock bitcoin would receive if all the sudden everyone is asked to pay $25 per transaction.
There is no evidence to suggest this is happening at scale, but fees went up yesterday from around $1 to around $4 for a normal transaction. It could be ordinary demand, but it could also be someone or some entity which wants to send bitcoin crashing.
They have succeeded as far as bitcoin’s sole purpose of moving bitcoins around is concerned because around 200,000 bitcoins have been stuck for the past 24 hours while fees have gone parabolic pricing everyone out.
Another Obituary?
Bitcoin has only one job — to move data from a to b — and it is failing to do that simple task. A task which is not really rocket science as some claim because everyone and their cat have launched their own bitcoin like network which actually manages to continue performing their one task.
No wonder bitcoin’s market share has now fallen down to around 48%, nearly halved from just a few months ago, but its price has now doubled to more than $2,000 and its market cap keeps going up, so, who knows. Maybe $20 fees and days for one transaction are a good thing?
Or maybe it’s all just because of the recent advertising following allegations Trump’s Press Secretary and an aid to the French President Macron had used bitcoin, combined with the recent ransom global incident.
Or perhaps it’s only because bitcoin is the main gateway to other altcoins, although ethereum has started making inroads on that front due to its own tokens system and clones.
But maybe the market sees value in a limited coin you just buy and lock away in some paper wallet somewhere, forgetting about it, like actual gold and just as difficult as well as expensive to move around.
In which case, “Bitcoin: A Peer-to-Peer Electronic Cash System,” as bitcoin’s white paper describes it, has failed, because the current bitcoin is not a cash system. Cash can be exchanged almost instantly with 0 fee and can be moved around fairly easily without getting stuck for days.
Which might be why the market is giving conflicting signals. On the one hand, it’s falling market share is probably because bitcoin investors and other market participants are looking for the real bitcoin, the cash system, which many think has just changed its name to ethereum while getting some cool new tech like smart contracts.
It may be that these newcomers think bitcoin is still the cash system rather than seemingly having changed into something else, or maybe they like this idea of gold but with very high fees or they’re in markets which have no choice, although even they could easily diversify.
Bitcoin is Dead, Long Live Bitcoin
So, to conclude, bitcoin is definitely in crisis because the real bitcoin as described in the whitepaper does not exist anymore. The real bitcoin uses the first seen rule for transactions, rather than ordering by fee. The real bitcoin never operates at full blocks. The real bitcoin has as good as no fees and confirms almost instantly.
What now is called bitcoin is an aberration, something completely different and planned to become even more different. Far more similar to ripple with its hubs and intermediary banks than to bitcoin.
The real bitcoin, the digital cash, the codable money, the global, inclusive, permissionless network, the innovative powerhouse which has grabbed the world’s imagination, that has changed its name and is now called ethereum.
Disclaimer: The views expressed in the article are solely that of the author and do not represent those of, nor should they be attributed to CCN.
David Ogden
Entrepreneur
Alan Zibluk Markethive Founding Member
